Розпочнемо з експерименту. У парку стоїть порожня лавка. Людина підходить до неї і сідає. Як ви думаєте, вона сяде на краєчку чи посередині? У більшості випадків ні там, ні там. Абсолютно інстинктивно людина сідає так, що відношення тієї частини лавки, яка буде праворуч від неї, до тієї, що буде ліворуч, становитиме близько 1,6.
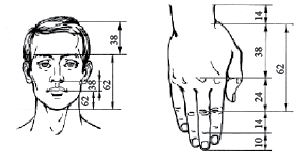
А тепер виміряйте відстань від кінчиків пальців до зап’ястя і від зап’ястя до ліктя, поділіть більше число на менше. Який результат?
Можна спробувати ще зіставити довжину пальців і всієї долоні, ширину і висоту обличчя, ширину носа і відстань між ніздрями, або багато інших розмірів (див. мал. 1).
Мал. 1. Пропорції тіла людини
Розміри будуть різні (у людей різної статі, віку, статури), але відношення розмірів стійко коливатиметься навколо числа 1,6 (приблизно як відношення 62 до 38). Якщо ж наявна точна пропорція, то зовнішність або тіло людини вважають ідеальним.
А тепер розглянемо кілька знайомих нам форм. Одна з найпоширеніших — це спіральна форма. Відразу пригадуємо черепашку молюсків чи хатку равлика? Але ця форма спостерігається повсюдно: у будові завитка внутрішнього вуха людини, рогу барана, хвоста морського коника й молекули ДНК, у русі смерчу й торнадо, виру та хвиль, галактик і комет, у розміщенні насінин соняшника, пелюсток маргаритки, квіток на стеблі конвалії, лусочок у ялинковій шишці.

Якесь дуже знайоме число виходить, чи не так?
Понад 800 років тому великий математик пізнього Середньовіччя монах Леонардо Пізанський (історично відомий як Фібоначчі) відкрив дуже цікаву послідовність чисел. Кожне наступне число є сумою двох попередніх: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610… і так до нескінченності.
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13…
Коли більше число з цієї послідовності поділити на менше число, розміщене поряд, то, починаючи з третього, співвідношення коливатиметься знову ж таки в межах 1,6; а якщо менше число поділити на більше число, яке стоїть поряд, то отримаємо приблизно 0,6 (тобто на одиницю менше).
Ми вже частково переконалися, що цю пропорцію можна побачити всюди в живій і неживій природі, а також — у живописі, скульптурі, архітектурі, музиці. Називають її по-різному: «золотою», «божественною», «золотим числом» тощо.
Талановиті майстри стародавньої Греції та Єгипту в основу багатьох своїх творів мистецтва клали «золоті пропорції». Золотий перетин — це такий пропорційний поділ відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама більша частина відноситься до меншої. При цьому коефіцієнт пропорції той самий — 1,6.
a:b = c:a ≈ 1,6
Мал. 3. Золоті пропорції в геометрії
Золотий прямокутник: якщо коротка сторона прямокутника дорівнює 1, то його довга сторона дорівнює 1,6; золотий трикутник — рівнобедрений трикутник, у якого бічні сторони відносяться до основи з коефіцієнтом 1,6. Вони це робили переважно інтуїтивно. Але чому? Тому що, як виявилося, при такій пропорції людині найприємніше дивитися на предмет дизайну, така пропорція найбільше відповідає естетичному сприйняттю людини. Щоправда, є люди, які не вбачають цієї закономірності й не сприймають золотий перетин як оптимальний, однак численні дослідження показали, що більшість опитаних віддали перевагу тим зображенням чи предметам, пропорції яких лежали в межах від 1,414 до 1,732. Що не кажіть, а золотий перетин входить у цей діапазон.
Так, портрет Мони Лізи (Джоконди) довгі роки привертає увагу дослідників, які виявили, що композиція малюнка заснована на золотих трикутниках, що є частинами правильного зірчастого п’ятикутника.
Одним із найкрасивіших творів старогрецької архітектури є Парфенон (V ст. до н. е.), який також збудовано з урахуванням золотих пропорцій.
Мал. 5. Парфенон в Афінах, Греція
Але повернімося до живої природи. Надзвичайно цікавим явищем є те, що послідовність чисел Фібоначчі спостерігається в спіральному розташуванні листків навколо стебла рослин. Учені називають це філлотаксисом. Цю спіральну форму добре видно, коли подивитися на стебло зверху, тоді можна побачити, що кут розходження листків від одного до іншого утворює частину вписаного кола. І в кожному випадку кут розходження відповідає числу з послідовності Фібоначчі. Наприклад: у в’яза кут розходження листків становить 1/2 кола; у берези й лісового горіха — 1/3; у абрикоси й дуба — 2/5; у груші й тополі — 3/8; у мигдального дерева й верби — 5/13; а в деяких сосен — або 5/21, або 13/34. Таке розміщенні дозволяє кожному листку отримати максимальну кількість сонячного світла й повітря, при цьому не затіняючи й не притискаючи сусідні листки.
Таку схему можна виявити й у пелюсток багатьох квітів. Наприклад: лілія має 3 пелюстки, фіалка круглолиста — 5, дельфініум — 8, ромашка непахуча — 13, айстра — 21, ромен-зілля — 34, геленіум — 55, айстра новобельгійська — 89.
Помітили також, що в ящірки довжина хвоста так відноситься до довжини тіла, як 62 до 38.
Досконалою є форма бабки, яка також створена за законом золотої пропорції: відношення довжин хвоста і корпусу дорівнює відношенню загальної довжини до довжини хвоста.
Бактерії розмножуються в прогресії, яку можна накреслити у вигляді спіралі Фібоначчі.
Метеорити, врізаючись у поверхню Землі, формують впадини, які співвідносяться зі спіраллю Фібоначчі.
Ми знаємо, що інформація, необхідна для утворення форм живих організмів, зберігається в їхніх ДНК, тому не дивно, що ширина молекули ДНК складає 21 ангстрем, а довжина повного повороту її спіралі дорівнює 34 ангстремам (обидва числа належать до послідовності чисел Фібоначчі).
Таким чином, золота пропорція проявляється в найрізноманітніших формах, числах і схемах, існує в найкрихітніших і найбільших частинах природи. Сама її присутність ставить під сумнів думку про те, що все виникло в ході еволюційних процесів, оскільки випадок не може створити таких складних взаємозв’язків, тим більше повторити їх багато разів у різних явищах природи та живих організмах. Це може бути лише творінням усемогутнього й премудрого Бога, що свідчить про Його досконалу майстерність, любов до краси й порядку. Це той самий Бог Біблії, про якого написано, що Він «вчиняє великі діла, яких не розуміємо ми» (Йов. 37:5). Це Ісус Христос, який єдиний достойний поклоніння: «Достойний Ти, Господи й Боже наш, прийняти славу, і честь, і силу, бо все Ти створив, і з волі Твоєї існує та створене все!» (Об. 4:11).
Поняття «золотого перетину», числовий ряд Фібоначчі входять до шкільної програми, але багато в чому саме від викладу вчителя залежить, що побачить у них дитина: дивне число з багатьма знаками після коми, загадку природи чи почерк геніального Творця Всесвіту?
Матеріал підготувала Надія Доля